Theoretical Computer Science

The generated production

In the history of thousands of years, people have studied a variety of calculations and found a lot of algorithms, but calculate or algorithm itself. The nature of the study is the mathematical theory of the study, but it has developed from the 1930s. At that time, in order to solve certain theoretical issues of mathematical foundation, whether or not there is a problem that the algorithm can be solved, the number of different (later proven is the equivalent) algorithm definition, thus establishing algorithm theory (Ie calculated theory). In the 1930s, K. Gotel and S.c. Clinney et al. Established a recursive function, and the algorithm of the origin function can be calculated as a recursive. In the mid-1930s, A.m. Turing and E.L. Perster independently proposed the concept of ideal computers, scraping the problem's algorithm to solubility on a desired computer with strict definition. The algorithm theory developed in the 1930s has an impact on the design idea of ​​storage program-type computers in the late 1940s. One of the ideal computer (called a charter) proposed by Tuling is a storage program type.

Discipline content

In these areas, automaton theory and form language theory is developed in the 1950s. The former history can also be trapped back to the 1930s because the Charter is a class of automaton (unlimited automaton). Some scholars since the 1950s began to consider the ideal computer with real-world computers, J. Nuiman proposed the concept of computer with self-propagation function in the early 1950s. Wang Hao puts forward a variant of a chartering machine in the mid-1950s, which is a machine that is more close to the real machine than the original map foreground. He also proposed a machine that cannot be cleared on the storage tape and proves that this machine is equivalent to the map of the chart. In the early 1960s, some people proposed a computer (referred to as RAM) with a random access memory and a multi-band chart.

Form Language Theory

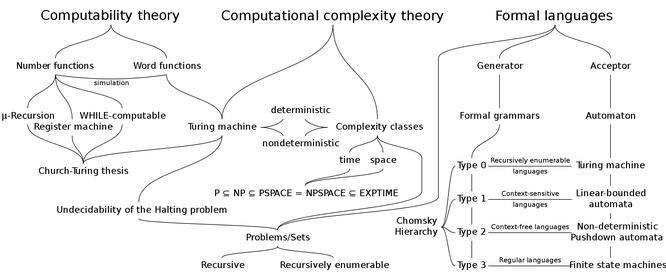
Guide from the Jumsky Theory in Mathematics. In this theory, the formal language is divided into four types: 10-type language; 21 type language; 32 language; 43 language. There is correspondingly in the case of type 0, type 1, type 2, and 3 types. Type 1 language is also known as the language, 2 language is also known as the context, and the 3-type language is also named regular language. The 2nd language is most attention. In the mid-1960s, the correspondence between the four languages ​​and four types of automators have also found (see table)

in the above table, the language listed on the left is exactly the automatic one and corresponding The language that can be identified (see form language theory).

Program Design Theory

includes program correctness certificates and program verification, some of its basic concepts and methods are proposed by Novaman and Tu Ling and others during the 1940s. Nogan, etc., in a paper proposes a method of verifying the correctness of the program by means of proof. Later, Tu Le proved the correctness of a subroutine. His method is to provide a given program, and there are variables x1, x2, ..., xn, and input predicate P (x1, ..., xn) and output predicate q (x1, ..., xn). If the following facts can be proven: If the program is established for pre-predicate P (X1, ..., XN), after the program is executed, the predicate Q (X1, ..., XN) is established, the correctness of the program.

Tulex's results have not attracted attention until P. Naur, in 1963 and EF Ferloud re-raised this method in 1966, it caused the attention of the computer science. . Since then, many theoretical workers are engaged in this area. However, as E.W. Daxtra has pointed out in the mid-1970s, the actual and effective method is to verify while designing, which proof or verification process is also ending at the same time. J. T. Schwatz and M. Davis have proposed a software technology they call "correct procedures technology" in the late 1970s. This method is to first select thousands of basic program modules and ensure the correctness of these basic programs with known various verification methods (including program correctness prove). Then, a set of programs that maintain the correctness can then be proposed. In this way, a variety of procedures can be generated by a constant combination.

It is pointed out that the "Circulating Unregory" developed by the program correctness, that is, the predicate attached to the entrance or exit point in a program in a program, some literature "Ingestted to assert", can be used for procedure research. That is, it is not as in the past, finding a given program to find a few cyclic uncarreans, and then prove the correctness of this program by these invariations; but before the program, according to this The requirements of a program, find a few cyclic invariance, then generate this program based on these invariance.

The concept of automatic programming is also proposed since the 1940s. In a paper in 1947, Tuling proposed a way to design the procedure. His idea is approximately as follows: set up a program to make a program that calculates a given recursive function f (x), and make f (n) = m (here N is either natural number, m is natural) Find a constructive certificate that demonstrates F (n) = m. After having such a constructive certificate, the F (X) evaluation algorithm can be extracted from this proof, and then the required procedure is generated. This thought is not known for a long time. In 1969, some people have filed this idea independently.

The formal grammar of the program language has been developed from the mid-1950s. The research of form semantics has made several different semantics theories since the 1960s, which proposes several different semantics theories, mainly for semantics, representation of semantics, and algebraic and algebraic. Semantics, but there is still no form of semantics that is recognized in software technology, and therefore need to be proposed more suitable for new semantics in actual calculations.

Program logic applied in the correctness of programming and form in form is developed in the end of the 1960s. This is an expansion of predicate logic. In the original predicate logic, there is no time concept, the reasoning relationship considered is the relationship at the same time. The program is a process, and the logical relationship between the input predicate of a program and the output predicate is not the relationship between the same time. Therefore, in the reason of the programs, the original predicate logic is not enough, and there is a new logic.

The end of the 1960s, E. Engel et al. found algorithm logic. C.A.R. Hall also created a program logic. This logic is obtained by adding a program operator in its original logic. For example, the program can be placed as a new operator in front of a predicate formula, such as expression

{s} p (x1, ..., xn) indicates that the predicate is predicted when the program S is executed. P (x1, ..., xn) is established (here) x1, ..., XN is the variable in the program S).

Algorithm Analysis and Computational Complexity Theory

About the Complexity of Algorithm. The names in this area have argued. It is generally believed that the study of the complexity of various specific algorithms is called algorithm analysis, and the study of general algorithm complexity is called computational complexity theory. Computational complexity Theory is originally a calculated theory, which is the computational complexity of various can compute functions (ie, recursive functions) (early as "calculated difficulty") for its research object. Calcible divided into two kinds of theoretical cursive and actual calculated. As a computable theory, the complexity theory is the complexity of the former, and the complexity theory of a field of computer science is the complexity of the latter.

The basic problem of this branch is to figure out the structure and some properties of the actual calculation of the functional class. Actual calculated is an intuitive concept. How to accurately describe this concept is an incapaci problem. Since the mid-1960s, relevant research workers generally use a functionally calculated function in computational time polynomial. This is actually a topic, rather than a proposition that can be proved or affirms in mathematics. It is pointed out that it is difficult to say that it is actually calculated when the number of polynomial times is higher (such as N).

Another fundamental problem is: Comparison of the problem of determining the problem of determining the problem of determining machine and non-deterministic machine. It has long been known that the problem of determining the problem of the problematic chart and the non-deterministic map of the chart is equal. Because the non-deterministic machine is higher than the deterministic machine efficiency, if the calculation time is not limited, the deterministic machine can always use the exhaustive method to simulate the non-deterministic machine. Therefore, the solitary ability of the two is the same. However, when calculating the time polynomial is bound, the two problem-like power is equal, this is a famous P =? Np problem.

About the calculation and algorithm (including procedures), more research on serial calculation, and research on parallel computing properties is still very insufficient (especially for asynchronous parallel calculations. ). Therefore, research on parallel computing is likely to be a research focus of computer theory.