Priori probability

Introduction

InBayesianstatisticalinference,thepriorprobabilitydistributionofanuncertainnumberisaprobabilitydistributionthatexpressesthedegreeofconfidenceinthenumberbeforeconsideringsomefactors.Forexample,thepriorprobabilitydistributionmayrepresenttheprobabilitydistributionoftherelativeproportionofvoterswhovotedforaparticularpoliticianinfutureelections.Theunknownquantitycanbeaparameterofthemodeloralatentvariable.

Bayes'theoremcalculatesthesuccessiveproductoftherenormalizationofthepriorandthelikelihoodfunctiontoproducetheposteriorprobabilitydistribution,whichistheconditionaldistributionoftheuncertaintyofthegivendata.

Similarly,thepriorprobabilityofarandomeventoranuncertainpropositionisanunconditionalprobabilityassignedbeforeanyrelevantevidenceisconsidered.

Therearemanywaystocreatepriorities.Thepastinformationcanbedeterminedbasedonpreviousexperiments.Previousexperiencecanbedrawnfrompurelysubjectiveassessmentsbyexperiencedexperts.Whennoinformationisavailable,anunknownpriorcanbecreatedtoreflectthebalancebetweentheresults.Theprioritycanalsobeselectedaccordingtocertainprinciples,suchassymmetryormaximizingtheentropyofagivenconstraint;examplesarethereferenceexamplesbeforeJeffriesorBernard.Whenthereisafamilyofconjugatepriors,selectthepreviousmethodfromthisfamilytosimplifythecalculationoftheposteriordistribution.

Theparameterofthepreviousdistributionisakindofhyperparameter.Forexample,ifthebetadistributionisusedtosimulatethedistributionoftheBernoullidistributionparameterp,then:

pistheparameteroftheunderlyingsystem(Bernoullidistribution),andαandβarethepreviousdistributions(βdistribution)parameter.

Hyper-parametersmaythemselveshavesuper-deriveddistributionsthatexpressbeliefsabouttheirvalues.ABayesianmodelwithmultiplepreviouslevelsiscalledahierarchicalBayesianmodel.

Informationprior

Informationpriorexpressesspecificandclearinformationaboutvariables.Takeanexample:thetemperaturedistributionbeforenoontomorrow.Areasonablemethodistosettheexpectedvalueofthenormaldistributiontobeequaltotoday'snoontemperature,anditsvarianceisequaltothedailychangeofatmospherictemperature,orthetemperaturedistributiononthatdayoftheyear.

Thisexamplehasmanyaprioricommonfeatures,thatis,frombehindonequestion(today'stemperature),becomesaprecedentforanotherquestion(tomorrow'stemperature);thepre-existingevidencethathasbeenconsideredisTheformerpart,andasmoreandmoreevidenceaccumulates,thelatterismainlydeterminedbyevidenceratherthananyoriginalhypothesis,providedthattheoriginalhypothesisacknowledgesthepossibilityofwhattheevidenceis.Theterms"previous"and"post"aregenerallyrelativetoaspecificbenchmarkorobservation.

Unknowingpriors

Unknowingpriorsrepresentvagueorgeneralinformationaboutvariables.Theterm"unknowingapriori"issomewhatcalledamisnomer.Suchapriorimayalsobecalledapriorithatisnotverypromising,thatis,itisnotasubjectivelyelicitedgoal.

Unknowinglyaprioricanexpress"objective"information,suchas"variableispositive"or"variableislessthanacertainlimit."Thesimplestandoldestrulefordeterminingunknowingaprioriistheprincipleof"indifference",whichassignsequalprobabilitiestoallpossibilities.Intheparameterestimationproblem,theuseofanuninformedpriorusuallyproducesresultsthatarenottoolargefromtraditionalstatisticalanalysis,becausethelikelihoodfunctionusuallyproducesmoreinformationthananuninformedprior.

Therehavebeensomeattemptstofindaprioriprobability,thatis,inasense,theprobabilitydistributionlogicallyrequiredbythenatureofthestateofuncertainty;thesearetopicsofphilosophicalcontroversy,andBayesisroughlydividedintotwoOne:"ObjectiveBayes",theybelievethatsuchprerequisitesexistinmanyusefulsituations,"SubjectiveBayes"whobelievethatinpractice,aprioriusuallyrepresentssubjectivejudgmentsandjudgmentscannotberigorouslyproven(Williamson2010).PerhapsthemostpowerfulargumentforobjectiveBayesianismisgivenbyEdwinT.Jaynes,mainlybasedontheconsequencesofsymmetryandtheprincipleofmaximumentropy.

Asanaprioriexample,considerasituationwhereapersonknowsthataballishiddeninoneofthethreecupsA,B,orC,butthereisnootherinformationaboutitslocation.Inthiscase,theuniformpriorofp(A)=p(B)=p(C)=1/3seemstobetheonlyreasonablechoice.Wecanseethatifweswapthelabelsofthecups("A","B"and"C"),theproblemremainsthesame.Therefore,itisstrangetochooseanapriori,inwhichthearrangementofthelabelswillleadtoachangeinourpredictionofwhichcupwillbefound;theaprioriistheonlyunitythatpreservesthisinvariance.Ifoneacceptsthisprincipleofimmutability,thenonecanseethatitwaslogicallycorrectbeforeunification.Itshouldbepointedoutthatthisusedtobe"objective"andrepresentsthecorrectchoiceforaspecificstateofknowledge,butitisnotobjective,butasanobserver'sindependentworldfeature:infact,theballexistsinaspecificcup.Next,ifthereareobserverswhohavelimitedknowledgeofthesystem,thenitmakessensetosaytheprobabilityinthiscase.

Amorecontroversialexample,Jaynespublishedanargumentbasedontheliegroup(Jaynes1968),whichshowsthatthefulluncertaintyofprobabilityshouldbep^-1(1-p)^-1.TheexamplegivenbyJaynesistofindachemicalsubstanceinthelaboratoryandaskwhetheritwilldissolveinwaterinrepeatedexperiments.Haldanepreviouslygavethemaximumweightofp=0andp=1,indicatingthatthesamplewilldissolveornot,withequalprobability.However,ifasampleofthechemicalhasbeenobservedtodissolveinoneexperimentandnotinanotherexperiment,itwaspreviouslyupdatedtoauniformdistributionontheinterval[0,1].ThisisobtainedbyapplyingBayes'theoremtoadatasetusingtheaforementionedpreviousdissolutionobservationandindissolutionobservation.Haldanewaspreviouslyanincorrectpriorassignment(meaningitdoesnotintegrateinto1).Ifalimitednumberofobservationsgivethesameresult,thenputthe100%probabilitycontentinp=0orp=1.HaroldJeffreys(HaroldJeffreys)designedasystematicdesignmethodforBernoullirandomvariables,suchasJeffreys'spreviousp^-1/2(1-p)^-1/2Appropriatepriorsthatthedesigndoesnotunderstand[theneedforclarificationdoesnotrequireeveryonetoagreewiththisstatement.

IftheparameterspaceXhasanaturalorganizationalstructurethatpreservesourBayesianstateofknowledge(Jaynes,1968),thenapriorproportionaltotheHaarmetriccanbeconstructed.Thiscanbeseenasageneralizationoftheprincipleofinvarianceusedtoprovetheuniformitybeforethefirstthreecupsintheaboveexample.Forexample,inphysics,wemayexpectthattheexperimentwillgivethesameresultregardlessoftheoriginofthecoordinatesystemwechoose.ThisleadstoagroupstructureoftranslationgroupsonX,whichdeterminesthepriorprobabilityasaconstantincorrectprior.Similarly,thechoiceofsomemeasurementsforanyscale(forexample,whethertousecentimetersorinches,thephysicalresultsshouldbeequal)willnaturallyremainthesame.

Incorrectprior

Makeeventsmutuallyexclusive.IfBayes'theoremiswrittenas

thenitisobviousthatifallpriorprobabilitiesP(Ai)andP(Aj)aremultipliedbyagivenconstant,thesameresultwillbeobtained;thesameistrueforcontinuousrandomvariables.Ifthesuminthedenominatorconverges,evenifthepreviousvaluedoesnotexist,theposteriorprobabilitywillstill(orintegral)be1.Therefore,thepriormayonlyneedtobespecifiedinthecorrectratio.Consideringthisideafurther,inmanycases,thesumorintegralofthepreviousvalues​​maynotevenneedtobefiniteinordertoobtainareasonableanswerfortheposteriorprobability.Inthiscase,itwaspreviouslycalledincorrect.However,ifthepriorisincorrect,theposteriordistributiondoesnotneedtobeanappropriatedistribution.ItisclearfromthefactthateventBisindependentofallAj.

Statisticianssometimesuseimproperpriorsasunknowingpriors.Forexample,iftheyneedapriordistributionofthemeanandvarianceofarandomvariable,theycanassumep(m,v)~1/v(forv>0),whichshowsthatanyvalueofthemeanis"probable",Andthevalueofthepositivevariancebecomes"lesslikely"inverselyproportionaltoitsvalue.Manyauthors(Lindley,1973;DeGroot,1937;KassandWasserman,1996)statedthatsincetheyarenotprobabilitydensities,theyriskover-interpretingthesepriors.Aslongastheyhaveacleardefinitionofallobservations,theonlycorrelationcanbefoundinthecorrespondingposterior.

Otherrelatedknowledge

Classificationofpriorprobability

Thepriorprobabilitycalculatedbyusingpasthistoricaldataiscalledobjectivepriorprobability;

Whenhistoricaldataisnotavailableorthedataisincomplete,thepriorprobabilityobtainedbyjudgingpeople'ssubjectiveexperienceiscalledsubjectivepriorprobability.

Conditionsofpriorprobability

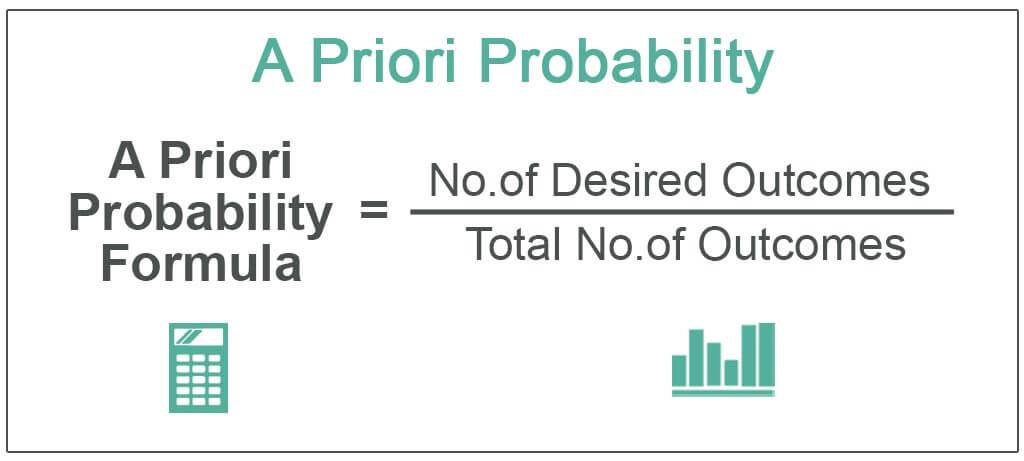
Priorprobabilityisdefinedbyclassicalprobabilitymodel,soitisalsocalledclassicalprobability.Theclassicalprobabilitymodelrequirestwoconditionstobemet:(1)allpossibleoutcomesoftheexperimentarelimited;(2)theprobability(probability)ofeachpossibleoutcomeisequal.IfthetotalnumberofallpossibleoutcomesisNandrandomeventAincludesnpossibleoutcomes,thentheprobabilityofrandomeventAisn/N.

Difference

Thepriorprobabilityisnotdeterminedbasedonallthedataaboutthenaturalstate,butonlycalculatedusingexistingmaterials(mainlyhistoricaldata);theposteriorprobabilityisusedFormorecomprehensiveinformationaboutthestateofnature,therearebothpriorprobabilitydataandsupplementarydata;

Thecalculationofthepriorprobabilityisrelativelysimple,andtheBayesianformulaisnotused;whilethecalculationoftheposteriorprobability,theBayesianformulaisused.Yees’formula,andwhenusingsampledatatocalculatelogicalprobability,thetheoreticalprobabilitydistributionmustbeused,whichrequiresmoreknowledgeofmathematicalstatistics.