Linearity constant system

Introduction

linear When the system is unchanged system

English: linear time invariant LTI)

It includes two definitions for continuous time systems and discrete time systems

concept

linear system has two definitions:

(1) Depending on whether the system's input and output relationships have linearity to define a linear characteristic that satisfy the principle. That is, if two excitation

(2) Defines a system consisting of linear elements and independent power supplies depending on the component characteristics of the system.

System nature

When the system is unchanged system

When the system is: the system's parameters do not change over time, ie The time of the input signal acts, the shape of the output signal response is the same, only from the time of occurrence. Use mathematics as T [X (n)] = y [n], T [N-N0)] = Y [N-N0], this shows that the sequence x (n) is shifted after transforming and The replacement is equivalent.

Linearity When the system

is linearly constant system: not only satisfy the stacking principle and the constant characteristics, it can be in unit pulse response Express. The unit impulse response is the system output when the input is the unit pulse sequence, which is generally represented as h (n), i.e., h (n) = t [Δ (n)].

Response y (n) = t [x (n)] = T [Δ (NK)];

Since the system is linear However, the above formula can be written into Y (N) = T [Δ (NK)];

is also due to the constant system, that is, T [Δ (NK)] = H (NK);

to obtain Y (n) = h (nk) = x (n) * h (n);

This formula is referred to as linear convolution, represented by "*".

Linear When the constant system

qi

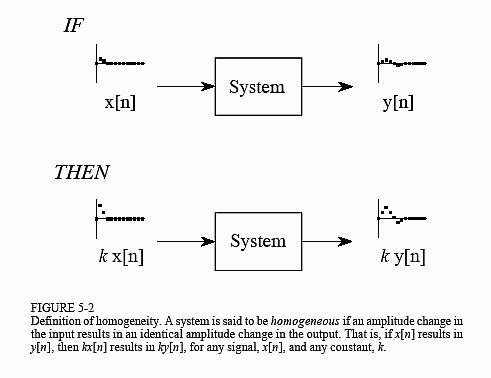
If the incentive F (t) is generated, Y (t) Then, the response generated by the excitation AF (T) is AY (T), which is homomive. Where A is any constant.

f (t) system y (t), AF (T) system AY (T)

superposition

If the excitation F1 (T) and F2 The response generated by (t) is Y1 (t), y2 (t), respectively, the sound

generated by the excitation F1 (T) + F2 (T) should be Y1 (t) + Y2 (T) This is called superposition.

Linear

If the responses generated by the excitation F1 (T) and F2 (T) are Y1 (t), Y2 (t), respectively, the A1F1 (T) + A2F2 ( T) The response of

is A1Y1 (T) + A2Y2 (T), which is called linear.

When the response generated by the excitation f (t) is Y (T), the response generated by the excitation F (T0) is Y (T-T0). ), This property is called

invariance, and regular or delay is also known. It illustrates that when the f (t) delay time T0 is excited, its response y (t) also delay

delay time T0, and the waveform is unchanged.

Differential

If the response generated by the excitation f (t) is Y (t), the response of the excitation f '(t) is Y' (t), this property That is, it is differential.

Pointability

If the response generated by the excitation f (t) is Y (t), the integration of the excitation F (t) is called Y (t). . This property is called integrated.