Infrared radiation

Abriefhistoryofinfraredradiation

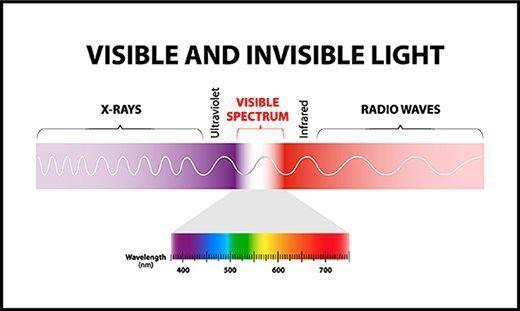
In1666,BritishphysicistI.Newtondiscoveredthatsunlightsplitsintocoloredlightbandsafterpassingthroughaprism-red,orange,yellow,green,andblue,Blue,purple.In1800,whenBritishastronomerF.W.Herschelstudiedthethermaleffectofthesolarspectrumwithamercurythermometer,hefoundthatthemostsignificantpartofthethermaleffectwasnotinthecoloredlightband,butoutsidetheredlight.Therefore,hebelievesthatthereisaninvisiblelightbesidestheredlight.Laterexperimentsprovedthatthisinvisiblelighthasthesamephysicalpropertiesasvisiblelightandobeysthesamelaws.Theonlydifferenceisaphysicalparameter—wavelength.Thisinvisiblelightiscalledinfraredradiation,alsocalledinfraredlightandinfraredlight.

Inthe17thand18thcenturies,manyphysicistsbelievedthatlight(includinginfraredlightandultravioletlight)hadafluctuatingnature,hadacertainpropagationspeed,andwavelengthwasitscharacteristicparameterandcouldbemeasured.Thedifferentcolorsofvisiblelightreflecttheirdifferentwavelengths.Violetlighthastheshortestwavelength,redlighthasthelongestwavelength,infraredradiationhasalongerwavelength,andultravioletlighthasashorterwavelengththanpurplelight.In1864,theBritishphysicistJ.C.Maxwelltheoreticallysummarizedtheexistinglawsofelectromagneticsatthattimeandproposedthepossibilityofelectromagneticwaves.Itspropagationspeedcanbecalculatedbypureelectricalquantities.Lateractualmeasurementsprovedthatitspropagationspeedisthespeedoflight.Therefore,itisconjecturedthatlightwavesareelectromagneticwaves.In1887,GermanscientistH.R.Hertzconfirmedthisconjecturewithexperiments.

Itisknownthatchargedobjectsemitelectromagneticwaveswhentheyaredisturbed.Thestrongerthedisturbance,thegreatertheenergyemittedbytheelectromagneticwave,andtheshorterthewavelength.Sincetherearemanywaysofbeingdisturbed,electromagneticwaveshaveawiderangeofwavelengths.Thenameandwavelengthrangeofeachbandoftheentireelectromagneticspectrum(seecolorpicture).

Infraredradiation

Infraredradiationislocatedinthecenteroftheelectromagneticspectrum,anditswavelengthcoversfourordersofmagnitude.Intheentireelectromagneticspectrum,nomatterwhichbanditis,itspropagationspeedisthespeedoflightc,thewavelengthisλ(cm),andthenumberofvibrationspersecondiscalledthefrequencyν(second-1),then

λν=c(1)

Dividingtheelectromagneticspectrumisdividedintomanybandswithdifferentnames.Theyaredividednaturallyaccordingtotheirproductionmethods,transmissionmethods,measurementtechniquesandapplicationranges.Infraredbandscanbedividedintothreebands:near-infrared,mid-infrared,andfar-infrared.However,themethodofclassificationvariesfromdisciplinetotechnicalfield.

Duetotheabsorptionofinfraredradiationbytheatmosphere,onlythree"windows"areleft,namely1to3microns,3to5microns,and8to13microns,whichallowinfraredradiationtopassthrough.Therefore,inmilitaryapplications,thesethreebandsarecallednear-infrared,mid-infrared,andfar-infrared.8-13microns,alsoknownasthermalband.

Inspectroscopy,themethodofdividingbandsisnotunifiedyet.Generally,0.75to3microns,3to40micronsand40to1000micronsareusedasthenear-infrared,mid-infraredandfar-infraredbands,respectively.Near-infraredisabandthatcanbedetectedbyusingglassasatransmissionmaterialandleadsulfidedetectors.Themid-infraredwasoriginallybasedonaprismasthewavelengthbandofthedispersiveelement,butlatergratingswereusedasthedispersiveelement,andthelimitof40micronsisnolongermeaningful.However,40micronsisthestartingwavelengthatwhichquartzcantransmitinfraredradiation,soitcanstillbeusedastheboundarybetweenthemid-infraredbandandthefar-infraredband.Atthelong-waveendofthefar-infraredband,traditionalgeometricopticsandmicrowavetransmissiontechnologiesarenotapplicable,andnewtechnologiesneedtobedeveloped.Thebandtowhichthenewtechnologyisapplicablemayalsobeabandwithanewname.Inaddition,lasersappearinthefar-infraredband,andwhethertheradiationsourcehascoherenceasthestandardfordemarcationbetweenfar-infraredandmicrowavesisnolongerapplicable.Therefore,1000micronsistemporarilyusedasthelimitofthefar-infraredband,andelectromagneticwaveswithawavelengthof1to3millimetersarecalledshortmillimeterwaves.

Generationofradiation

Insidematter,electrons,atoms,andmoleculesareconstantlyinmotion,andtherearemanypossiblestatesofmotion.Thesestatesareallstableandeachhasacertainamountofenergy.Thesestatesareusuallyrepresentedby"energylevels".Undernormalcircumstances,matterisalwaysatthelowestenergylevel(groundstate).Ifthereisexternalstimulationorinterference,theappropriateenergycanbetransferredtoelectrons,atomsormolecules,thelattercanchangethestateofmotionandenterahigherenergylevel(excitedstate).However,electrons,atoms,ormoleculesstayintheexcitedstateforashorttime,andquicklyreturntoalowerenergylevel,releasingexcessenergy.Therearemanywaystoreleaseenergy,themostcommonistoemitelectromagneticwaves.Accordingtotheconceptofmodernquantumtheory,whenreturningfromahigherenergylevelE1toalowerenergylevelE0,thefrequencyoftheemittedelectromagneticwaveis

ν=(E1-E0)/h(2)

WherehisPlanck’sconstant,h=6.626×10-34Joule·sec,hνistheemittedenergyunit,calledForphotons.

Therefore,radiationisemittedfrommatter.Anysmallobjectcontainsahugenumberofatomsormolecules.Eachatomormoleculehasmanyenergylevels,andthetransitionfromahighenergyleveltoalowenergylevelcanemitphotons.Theelectromagneticwaveactuallyemittedisthesumoftheselargenumbersofphotons.Theprocessofeachatomormoleculeemittingphotonsisbasicallyindependentofeachother;thetimeofphotonemissionisfirstandthenlater.Whenaphotonisemitted,therearevariouspossibilitiesfortheorientationofatomsormoleculesinspace,sothephotoncanbeemittedinvariousdirections,anditselectromagneticfieldvibrationcanalsohavevariousdirections;coupledwiththemutualinfluencebetweentheenergylevelsintheobject,thetwoenergyTheenergydifferencebetweenthestageswillvaryslightly.Thecombinedeffectofallthesefactorsmakestheemittedradiationcontainvariousfrequencieswithoutacertainphaseorpolarization,whichisincoherentradiation.

Modernscienceandtechnologycanadoptappropriatemethodstoforcethephotonemissionprocessbetweencertaintwoenergylevelstooccurinthesamedirectionatthesametime.Thiswillresultinaverynarrowfrequencyband,excellentdirectivity,andintensity.Veryhigh,anditispolarizedcoherentradiation.Thisisthelaser.Intherangeofradiowavesandmicrowaves,thegenerationofelectromagneticwavesusesthemovementofelectronsinavacuumtoforceallelectronstochangeinthesamestateofmotion,whichemitssingle-frequency,polarizedcoherentradiation.

Althoughradiationisemittedfromtheinsideoftheobject,itmustfirstbedisturbedandgivenenergyfromtheoutsideworld.Thisprocessiscalledmotivation.Therearemanyexcitationmethods,amongwhichthemostcloselyrelatedtoinfraredradiationisheating.Theradiationemittedbyheatingiscalledthermalradiation.

InfraredradiometryTheterminologyinthisareaismorecomplicated.Itisnecessarytodistinguishbetweentheemissionandreceptionofradiationandindicatethedirectionalityoftheextendedsource.Anextendedsourceisaradiationsourcewhosesizeisnotnegligiblecomparedtothemeasureddistance.Onthecontrary,itcanbetreatedasapointsource.

Thenames,symbols,unitnamesandunitsymbolsofsomemajorradiometrictermsarelistedinthetable.

Infraredradiationradiance

Themostbasicphysicalquantitydescribingtheradiationsource.Itsdefinitionis:inthedirectionoftheangleθwiththenormalofthesurface(assumingithasnothingtodowiththeazimuthangleφ),theunitprojectedareaemitsintotheunitsolidangleRadiatedpower(Figure1).

Infraredradiation

whereωrepresentsthesolidangle.ThereisakindofobjectcalledLambertiansurface,fromitsfaceelementdA,theradiationpowerandcosθi>θisproportional:

Theformulaistheradiatedpowerintheunitsolidangleinthenormaldirection.(3)ThedefinitionoftheformulaiscalculatedbasedontheunitprojectedareadAcosθ,sothereis

• InfraredRadiationAtlas(1sheet)

• InfraredRadiationAtlas(1sheet)

Thatis,theradianceoftheLambertiansurfaceisthesameinanydirection,equaltothenormalradiance.Takingintoaccountthisfactorinthedefinitionofradiance,thetotalradiationpoweremittedfromthesurfaceelementdAintotheentireupperhemisphereshouldbe

where2πsrrepresentstheintegralrangeof2πsolidangle.

RadiationEmission

Thetotalradiantpoweremittedtotheupperhemisphereperunitarea.M=dφ/dA(W/m2)(6)

dφistheformula(5)Therequiredradiationpower,therefore

M=πL(7)

ForLambertiansurfaces,thisrelationshipisveryimportant.Inpractice,aslongastheradianceinthenormaldirectionismeasured,theradiantemissiondegreeMcanbeobtained.Fornon-Lambertiansurfaces,itisnecessarytomeasuretheradiatedpowertoalldirections,andthenintegratetoobtainM.

Radiationoutputreferstotheradiantpoweremittedfromaunitarea,whichcanbetheradiationemittedbytheobjectitself;itcanalsobetheradiationreflectedbytheobject.Theword"out"isemphasizedhere.Ifitreferstotheradiationprojectedonthesurfaceoftheobject,itmustbeexpressedintermsofirradiance.Bothhavethesamedimension.

Radiationintensity

Theradiantpowerwithintheunitsolidangleθwheretheentiresurfaceoftheemitterentersacertaindirectionθ

I=dφ/dω(W/sr)(8)

(3)IntegratetheareawiththeformulatogetI.Inthiscase,theextendedsourceisregardedasapointsource.Theuseofthewordintensitycanbeconsistentwiththecorrespondingtermsinotherpointsources(electricity,magnetism,andlight).

Radiantpower

Ithasthesamemeaningasradiantenergyflux,buttheusageisslightlydifferent.Itisappropriatetouseradiantpowerwhendiscussingradiationemittedorreceivedbyasurface.Whendescribingtheradiationinanimaginaryplaneofspace,radiantenergyfluxshouldbeused.

Thequantitieslistedinthetablerefertotheemissionofacertainspectrumoftheradiationsource,ifitistobedescribedatthewavelengthλandwithintheintervalλ,Ortheamountwithintheintervalofνatthefrequencyν,add"monochrome","spectrum"or"points"beforethenameofeachquantityinthetable.Spectrum",addλorνtothelowerrightfootofthesymbol,suchasθλ,ωλ,φλ,Iλ,Mλ,Lλ,Eλorθν,φν,Iν,Mν,Lν,Eνetc.Whendiscussingonlyacertainmonochromaticradiation,"monochromatic"shouldbeused.Whendiscussingtheamountofeachmonochromaticradiationintheentirespectrum,itisadvisabletouse"spectrum"or"spectrum"infront.

Becausethecomponentsofradiationarelinearlysuperimposed,therelationshipofM=πLisalsoapplicabletomonochromaticradiation

Mλ=πLλ(9)

Thermalradiationanditslawsheatupcertainmotionstatesinsidethematerialtoanexcitedstate.Whenthestatereturnstoalowerenergystate,radiationwillbegenerated,whichiscalledthermalradiation.Thiskindofradiationmaybeabsorbedbytheobjectagain,stimulatingsomemovementandthencausingheatradiation.Therefore,theheatradiationprocessmayreachastableequilibriumstate.Forexample,consideraclosedcavitywithwallsmadeofacertainmaterial.HeatingkeepsitataconstanttemperatureT0.Inthecavity,theradiationemittedbyanyfaceelementdAonthecavitywallalwaysfallsonanotherpartofthecavitywall.Theradiationfallingonacertainpartofthecavitywallispartlyabsorbed,andtherestisreflectedandfallsonanotherpartofthecavitywall.Therefore,nomatterwhichpartofthecavitywallemitsradiation,itwillalwaysenterthecavitywallintheend.Undertheconditionofreachingthermalequilibrium,theradiationproducedbyanypanelelementisalwaysequaltotheradiationabsorbedbyitintermsoffrequencyandintensity.Otherwise,itisnotthermalequilibrium.Therefore,inthecavityunderthermalequilibriumconditions,allradiationmusthaveastableandunchangingproperty,whichonlydependsonthetemperatureofthecavitywall,andhasnothingtodowiththenatureofthecavitywallmaterial.

Blackbodyradiation

Takeasmallobjectofanymaterialandputitintothecavitywithouttouchingthecavitywall.Soon,theobjectisheatedtothesametemperatureasthecavitywall,thatis,itreachesthermalequilibriumwiththecavitywall.Atthistime,theradiationemittedbythesurfaceofthesmallobjectmustbeequaltotheradiationabsorbedbyitintermsoffrequencyandintensity.SupposetheirradiancereceivedbythesurfaceoftheobjectisE(W/m2),theabsorptionratiooftheobjecttoradiation(theratiooftheabsorbedpowertotheincidentpower)isα,anditsradiationoutputisM(W/m2),foranypartofthesurface,thethermalequilibriumconditionis

M=αE(10)

Theaboveformulashowsthatthegreatertheabsorptionratioofanobjecttoradiation,thegreateritsradiationoutput,thatis,thestrongertheabsorptionoftheobject,thestrongertheradiation.ThisisKirchhoff'slaw.

Whenα=1,theradiationoutputreachesthemaximum.Objectswiththischaracteristicarecalledblackbodies.Theradiationitemitsiscalledblackbodyradiation.Theshouldermark"bb"intheupperrightcornerindicatestheamountofblackbodyradiation.

Whenα=1,theirradianceofobjectsinthecavityis

E=Mbb(11)

Inotherwords,theradiationinthethermalequilibriumcavityisblackbodyradiation.Therefore,theradiationemissiondegreeofanyobjectis

M=αMbb(12)

ItisalwayssmallerthantheradiationoftheblackbodyDegreeofemergence.

Blackbodiesarenotuncommon.Ifasmallholeisopenedinthecavitywall,theareaof​​theholeismuchsmallerthantheareaof​​thecavitywall,andtheradiationenergyemittedfromthesmallholeisverysmallandinsufficient.Toaffecttheheatbalanceinthecavity.Theradiationthatentersthesmallholefromtheoutsideisreflectedmultipletimesbythecavitywall,andisalwayscompletelyabsorbed,andisnolongerreflectedfromthesmallhole,sotheabsorptionratioisequalto1.Acavitywithasmallholeisablackbody,andtheradiationemittedfromthesmallholeisablackbodyradiation.

Blackbodyradiationisoneofthemoststudiedphysicsissuesattheendofthe19thcentury.Manymeasurementshavebeencarriedoutontheradiationemittedbythecavity,whichprovesthattheblackbodyradiationisofLambertiantype,anditsradiationpowerisstableaccordingtothewavelengthorfrequencydistribution,whichisonlyrelatedtothetemperatureofthecavitywall,andhasnothingtodowiththematerialofthecavity.Figure2showsthedistributioncurveoftheblackbody'sradiantemissionaccordingtothewavelengthatseveraltemperatures.Apeakappearsonthedistributioncurveofeachtemperature,andthewavelengthofthepeakλmshiftstoshortwavesasthetemperaturerises.

Infraredradiation

Twousefulempiricallawscanbeobtainedfromthemeasurementdata,namelyStefan’slawandWien’sdisplacementlaw.

Stefan’sLaw

Theblackbody’sradiationoutput,thetotalradiantpowerincludingvariouswavelengthsandtheblackbodytemperature(absolutetemperaturescale)TProportionaltothe4thpower

Mbb=σT4(/m2)(13)

σistheconstantofproportionality.TherelationshipofT4isderivedbyBoltzmannusingthermodynamicmethods.Therefore,thislawisoftencalledStefan-Boltzmann'slaw.TheproductofWien'sdisplacementlawpeakwavelengthλmandblackbodytemperatureTisaconstant

λmT≈3000

FromtheoryDeducingthedistributioncurveofblackbody'sradiationemissiondegreeversuswavelength(frequency)(Figure2)wasanextremelyimportantphysicstopicattheendofthe19thcentury.In1900,M.Planckproposedanewconcept,thatis,radiantenergyisnotcontinuousandcanonlybeabsorbedoremittedinacertainamount.Thisweightiscalledquantum(alsocalledphotonhere),anditisproportionaltothefrequencyofradiation.Thatis,theenergyofthephotonishν,andtheproportionalconstanthiscalledPlanck'sconstant.Later,accuratemeasurementprovedthath=6.626×10-34Joule·sec.

Infraredradiation

Planckusesthequantumconcepttoderive,andtheformulafortheblackbody'sradiationoutputis

or

Wherecisthespeedoflight;κisBoltzmann'sconstant.ThisformulaiscalledPlanck'slawofradiation.

Thisformulacanaccuratelyexplainalltheexistingexperimentaldata,anditalsoexpressestheconstantsintheabovetwoempiricalformulaswithmorebasicphysicalconstants.

Planck'sformulacannotonlyexplainalltheexperimentalfactsthatexistedatthattime,butalsoafterthe1960s,astronomersdiscoveredthattheuniverseisfullofatypeoflong-waveinfraredradiation,whosewavelengthdistributioniscompletelyinlinewithPlanck'sformula.Itisconsistent,whichprovesthatthereisabackgroundtemperatureof2.7Kintheuniverse.

TheblackbodyradiationcanbeaccuratelycalculatedwiththePlanckformula,soblackbodyhasbecomethestandardofradiationmeasurement.Variousformsofblackbodieshavebeenmanufactured,someofwhichareveryclosetoidealblackbodies.TheblackbodyradiationdatatablecalculatedaccordingtothePlanckformulahasbecomeamanualforinfraredengineeringdesigners.

Moreimportantly,Planck’squantumhypothesiscreatedthequantumphysicsofthe20thcentury.

Theheatradiationofgeneralobjects

Theabsorptionratioofgeneralobjectstoradiationisalwayslessthan1,sotheabilitytoemitheatradiationisalsolessthanthatofblackbodies.Foritsradiance,itisgenerallynotmeasureddirectly,butcomparedwiththeblackbodyradiationatthesametemperature,andaratioisusedtoexpressitsradiationcharacteristics.

Firstofall,comparetheradianceofaheat-radiatingobjectandablackbodyatthesametemperatureinalldirections.TheradianceoftheformerLcanbewrittenasL=ε,ψ)Lbb(16)

Intheformula,εiscalledemissivity,ε<1.Formostheat-radiatingobjectswithpracticalvalue,εhasnothingtodowiththedirection,ψ).Therefore,uptoclassobjectsalsohaveaLambertiansurface,andtherelationofM=πLisalsoapplicable.

Secondly,comparethenormalradianceofheat-radiatingobjectsandblackbodiesatvarioustemperaturesandwavelengths.Usingtheaboverelationship,theradiationemissiondegreeoftheobjectcanbeobtainedM

M=ε(T,λ)Mbb(T,λ)(17)

whereεisrelatedtowavelengthandheatThetemperatureoftheradiatorisrelated.However,forsomeheat-radiatingobjectswithpracticalvalue,thechangeofεwithλisrelativelyslow.Withintherequiredspectralrange,youcanregardεasaconstant,ortakeanappropriateaveragevalue.Inthisway,theStefan’slawobtainedbyintegratingthewavelengthaccordingtothePlanckformulacanbewrittenas

M=ε(T)σT4(18)

Therefore,foranyheatradiationobject,aratioεcanbeusedtodescribeitsheatradiationperformance.Generallyspeaking,εisacomplexfunctionofdirection,temperatureandwavelength.However,somecommonlyusedheatradiatorsmostlyhaveaLambertiansurface,andεchangesslowlywithλ.Useanε(T)isenoughtodescribeallitsthermalradiationcharacteristics.

Inthepreviousdiscussionofthecavitythermalbalance,weobtainedequation(12).Comparingitwithequation(18),weget

ε=α(19)

Thatis,theabsorptionratioandemissivityofanyobjectareequalatanytemperatureandanywavelength.Blackbodyisaspecialcase,ε=α=1.

Whenα<1,partoftheradiationprojectedonthesurfaceoftheobjectisreflected,andtherestentersthebodytobeabsorbed.However,itisalsopossiblethatonlypartofitisabsorbed,whiletherestradiatesthroughtheobject.Ifthereflectance(theratioofthereflectedradiationpowertotheincidentradiationpower)isρ,thetransmittance(theratiooftheradiationpowerthroughtheobjecttotheincidentradiationpower)isτ,accordingtothelawofconservationofenergy,thereshouldbe

α+ρ+τ=1(20)

Foropaqueobjectsτ=0,then

α+ρ=1

Therefore

ε=1-ρ(21)

Inpractice,themethodofmeasuringρisoftenusedtofindε.

Objectemissivitydata

Seethetablefortheemissivityofseveralcommonobjects.

Industrialapplications

Themainapplicationsofinfraredradiationare:infrareddetectors,infraredthermometers,infraredimagingtechnology,infrarednon-destructivetesting,andinfraredreconnaissanceandinfraredradarinthemilitary.Wait.Themostimportantapplicationsinindustryareinfraredthermometersandinfraredthermalimagingcameras.

Objectswithatemperatureaboveabsolutezerowillradiateinfraredraysduetotheirownmolecularmotion.Afterthepowersignalradiatedbytheobjectisconvertedintoanelectricalsignalbytheinfrareddetector,theoutputsignaloftheimagingdevicecansimulatethespatialdistributionofthesurfacetemperatureofthescannedobjectinaone-to-onecorrespondence,andisprocessedbytheelectronicsystemandtransmittedtothedisplayscreentoobtaintheThecorrespondingthermalimageoftheheatdistributiononthesurfaceoftheobject.Usingthismethod,itcanrealizethelong-distancethermalimageimagingandtemperaturemeasurementofthetarget,andanalyzeandjudgeit.Takingadvantageofthis,infraredthermometershavebeguntobecomethemainstreaminthefieldoftemperaturemeasurement.

Infraredthermalimagingcamerausesinfrareddetector,opticalimagingobjectivelensandopto-mechanicalscanningsystem(advancedfocalplanetechnologyeliminatestheopto-mechanicalscanningsystem)toreceivetheinfraredradiationenergydistributionpatternreflectionofthemeasuredtargetTothephotosensitiveelementoftheinfrareddetector,betweentheopticalsystemandtheinfrareddetector,thereisaphoto-mechanicalscanningmechanism(thefocalplanethermalimagerdoesnothavethismechanism)toscantheinfraredthermalimageofthemeasuredobjectandfocusontheunitOronthespectroscopicdetector,theinfraredradiantenergyisconvertedintoanelectricalsignalbythedetector,andtheinfraredthermalimageisdisplayedonaTVscreenormonitorthroughaTVscreenormonitorafteramplifying,converting,orstandardvideosignal.Thisthermalimagecorrespondstotheheatdistributionfieldonthesurfaceoftheobject.

Infraredthermometersandthermalimagingcamerasarewidelyusedinpowerplants,steelmills,large-scalemachinetools,powerinspections,forestfirepreventionandotherfields.