Information entropy

TheoreticalProposal

Inthepaper"AMathematicalTheoryofCommunication(AMathematicalTheoryofCommunication)"publishedin1948byCEShannon,thefatherofinformationtheory,thereisredundancyinanyinformation.Thesizeoftheremainderisrelatedtotheprobabilityoruncertaintyofeachsymbol(number,letterorword)inthemessage.

Shannondrawsontheconceptofthermodynamics,andcallstheaverageamountofinformationafterexcludingredundancyas"informationentropy",andgivesamathematicalexpressionforcalculatinginformationentropy.

Basiccontent

Usually,whatsymbolasourcesendsisuncertain,anditcanbemeasuredaccordingtotheprobabilityofitsappearance.Theprobabilityislarge,therearemanyopportunities,andtheuncertaintyissmall;otherwise,theuncertaintyislarge.

TheuncertaintyfunctionfisadecreasingfunctionoftheprobabilityP;theuncertaintygeneratedbytwoindependentsymbolsshouldbeequaltothesumoftheirrespectiveuncertainties,namelyf(P_1,P₂)=f(P₁)+f(P₂),thisiscalledadditivity.Thefunctionfthatsatisfiesthesetwoconditionsatthesametimeisalogarithmicfunction,namely.

Intheinformationsource,whatisconsideredisnottheuncertaintyofasinglesymbol,buttheaverageuncertaintyofallpossiblesituationsofthisinformationsource.Ifthesourcesymbolhasnvalues:U₁…U_i…U_n,thecorrespondingprobabilityis:P₁…P_i…P_n,andtheappearanceofvarioussymbolsareindependentofeachother.Atthistime,theaverageuncertaintyoftheinformationsourceshouldbethestatisticalaverage(E)oftheuncertaintyofasinglesymbol-logP_i,whichcanbecalledinformationentropy,thatis,,Thelogarithmintheformulagenerallytakes2asthebase,andtheunitisbit.However,otherlogarithmicbasescanalsobeused,andothercorrespondingunitscanbeused,andthebaseexchangeformulacanbeusedtoconvertbetweenthem.

Thesimplestsingle-symbolinformationsourceonlytakestwoelementsof0and1,thatis,abinaryinformationsource.ItsprobabilityisPandQ=1-P.TheentropyofthissourceisasshowninFigure1.Shown.

Ascanbeseenfromthefigure,theinformationentropyofadiscretesourcehas:

①Negative:theamountofinformationobtainedbyreceivingasourcesymbolshouldbeapositivevalue,H(U)≥0

②Symmetry:symmetricaltoP=0.5

③Certainty:H(1,0)=0,thatis,P=0orP=1Itisacertainstate,andtheamountofinformationobtainediszero

④Extreme:BecauseH(U)isanupwardconvexfunctionofP,andthefirstderivativeisequalto0whenP=0.5,sowhenP=0.5When,H(U)isthelargest.

Forcontinuousinformationsources,Shannongavecontinuousentropysimilarinformtodiscretesources.Althoughcontinuousentropyisstilladditive,itdoesnothavenon-negativeinformation.Sexisdifferentfromdiscretesources.doesnotrepresenttheamountofinformationofacontinuoussource.Thevalueofthecontinuousinformationsourceisunlimited,andtheamountofinformationisinfinite,andisafiniterelativevalue,alsoknownasrelativeentropy.However,whenthedifferencebetweenthetwoentropiesistakenasmutualinformation,itisstillnon-negative.Thisissimilartothedefinitionofpotentialenergyinmechanics.

Informationmeaning

Moderndefinition

Informationismaterial,energy,informationandThelabelofitsattributes.[InverseWienerInformationDefinition]

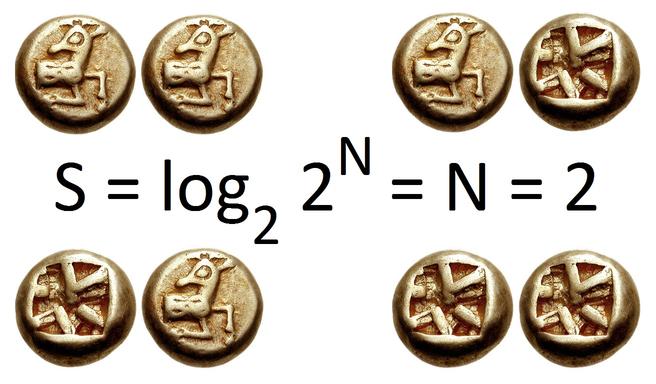
Informationisincreasedcertainty.[InverseShannonInformationDefinition]

Informationisacollectionofthings,phenomenaandtheirattributes.[2002]

Initialdefinition

ClaudeE.Shannon,oneoftheoriginatorsofinformationtheory,definedinformation(entropy)astheprobabilityofoccurrenceofdiscreterandomevents.

Theso-calledinformationentropyisaratherabstractconceptinmathematics.Herewemightaswellunderstandinformationentropyastheprobabilityofoccurrenceofacertainspecificinformation.Theinformationentropyandthermodynamicentropyarecloselyrelated.AccordingtoCharlesH.Bennett'sreinterpretationofMaxwell'sDemon,thedestructionofinformationisanirreversibleprocess,sothedestructionofinformationconformstothesecondlawofthermodynamics.Theproductionofinformationistheprocessofintroducingnegative(thermodynamic)entropyintothesystem.Therefore,thesignofinformationentropyandthermodynamicentropyshouldbeopposite.

Generallyspeaking,whenakindofinformationhasahigherprobabilityofoccurrence,itindicatesthatithasbeenspreadmorewidely,orinotherwords,thedegreeofcitationishigher.Wecanthinkthatfromtheperspectiveofinformationdissemination,informationentropycanrepresentthevalueofinformation.Inthisway,wehaveastandardformeasuringthevalueofinformation,andwecanmakemoreinferencesabouttheproblemofknowledgecirculation.

Calculationformula

H(x)=E[I(x_i)]=E[log(2,1/P(x_i))]=-∑P(x_i)log(2,P(x_i))(i=1,2,..n)

Amongthem,xrepresentsarandomvariable,whichcorrespondstothesetofallpossibleoutputs,definedasasymbolset,andtheoutputofarandomvariableisrepresentedbyx.P(x)representstheoutputprobabilityfunction.Thegreatertheuncertaintyofthevariable,thegreatertheentropy,andthegreatertheamountofinformationneededtofigureitout.

"TheBibleofGame"

InformationEntropy:InformationThebasicfunctionistoeliminatepeople'suncertaintyaboutthings.Aftermostoftheparticlesarecombined,valuablenumbersarestakedonitsseeminglynon-imageform.Specifically,thisisaphenomenonofinformationconfusioninthegame.

Shannonpointedoutthatitsaccurateamountofinformationshouldbe

-(p1*log(2,p1)+p2*log(2,p2)+...+p32*log(2,p32)),

Amongthem,p1,p2,...,P32aretheprobabilityofthe32teamswinningthechampionshiprespectively.Shannoncalledit"Entropy"(Entropy),generallyrepresentedbythesymbolH,andtheunitisbit.

Interestedreaderscancalculatethatwhen32teamshavethesameprobabilityofwinning,thecorrespondinginformationentropyisequaltofivebits.Readerswithamathematicalfoundationcanalsoprovethatthevalueoftheaboveformulacannotbegreaterthanfive.ForanyrandomvariableX(suchasthechampionshipteam),itsentropyisdefinedasfollows:

Thegreatertheuncertaintyofthevariable,thegreatertheentropy.TofigureouttheinformationneededThegreatertheamount.

Informationentropyisaconceptusedtomeasuretheamountofinformationininformationtheory.Themoreorderlyasystem,thelowertheinformationentropy;

Conversely,themorechaoticasystem,thehighertheinformationentropy.Therefore,informationentropycanalsobesaidtobeameasureofthedegreeofsystemorder.

Theconceptofentropyisderivedfromthermalphysics.

Assumingthattherearetwokindsofgasesaandb,whenthetwogasesarecompletelymixed,thestablestateinthermophysicscanbereached,andtheentropyisthehighestatthistime.Ifthereverseprocessistoberealized,thatis,thecompleteseparationofaandbisimpossibleinaclosedsystem.Onlyexternalintervention(information),thatis,addingsomethingorderly(energy)outsidethesystem,separatesaandb.Atthistime,thesystementersanotherstablestate,atthistime,theinformationentropyisthelowest.Thermalphysicsprovesthatinaclosedsystem,theentropyalwaysincreasestothemaximum.Toreducetheentropyofthesystem(makethesystemmoreorderly),theremustbeexternalenergyintervention.

Thecalculationofinformationentropyisverycomplicated.Theinformationwithmultiplepreconditionsisalmostimpossibletocalculate.Therefore,thevalueofinformationintherealworldcannotbecalculated.Butbecauseoftheclosecorrelationbetweeninformationentropyandthermodynamicentropy,informationentropycanbemeasuredintheprocessofattenuation.Therefore,thevalueofinformationisreflectedthroughthetransmissionofinformation.Withouttheintroductionofaddedvalue(negativeentropy),thewiderthespreadandthelongerthespreadingtime,themorevaluabletheinformation.

Entropyisfirstofallanouninphysics.

Incommunication,itreferstotheuncertaintyofinformation.Theentropyofahighdegreeofinformationisverylow,andtheentropyofalowdegreeofinformationishigh.Specifically,anyactivityprocessthatleadstoanincreaseordecreaseinthecertainty,organization,regularity,ororderofthesetofrandomeventscanbemeasuredbytheunifiedscaleofthechangeininformationentropy.