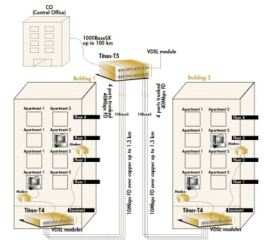
Full name quantifier

Note

In some full-term propositions, sometimes the full-scale quantifier can be omitted. For example, the prism is a polyhedron, which refers to "any prismatic multifisament".

1, "for full", "any" words in the logic are called full name quantifier , remember "∀", proposition containing full name Celebrate full name proposition .

For any any x in m , there are p ( ) is established , record it ∀ x ∈ M, P (x)

reading: For any xbelonging to M, it has P ( x ) was established.

2, "There is one", "at least one", "at least one", etc., is called existence , remember to "∃", is called Special proposition .

m existence 1 x , make P ( ) is established , recorded as ∃ x ∈ m

reading: reading: There is a x belonging to m , making P ( x ) is established.

Negative:

1, For a full name proposition containing a quantifier P : ∀ x ∈ m , p ( x ) negation P x ∈ m , ┐P (x).

2, for the P P : ∃ x ∈ m , p ( x ) negation p is: ∀ x ∈ m , ┐P (x).

full name proposition

full name proposition: its formula is "full s is p ".

full-term proposition, you can use a full name quantifier, you can also express it through the "human" and other subjects, or even any quantifier logo, such as "human beings are wisdom."

Since the algebraic theorem is a full name quantifier, each algebraic theorem is a full name proposition. It is also a full name quantifier to make the use of the brought rules for constant transformations are the core of algebraic reasoning.