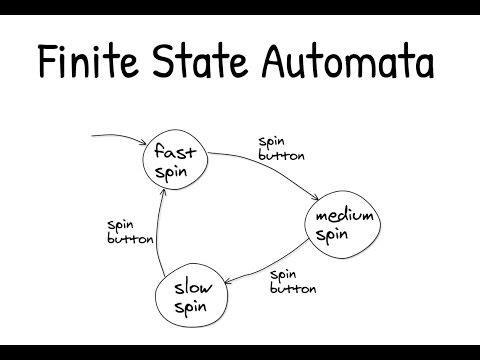
Finite state automata

Mainfeatures

Finitestateautomataisamathematicalmodelofasystemwithdiscreteinputsandoutputs.

Themainfeaturesareasfollows:

–(1)Thesystemhasafinitenumberofstates,anddifferentstateshavedifferentmeanings.Accordingtoactualneeds,thesystemcancompletethespecifiedtasksindifferentstates.

–(2)Wecancombinethecharactersthatappearintheinputstringtoformanalphabet.Allstringsprocessedbythesystemarestringsonthisalphabet.

–(3)Inanystate,thesystemreadsacharacterfromtheinputstring,andtransferstoanewstateaccordingtothecurrentstateandthereadcharacter.

–(4)Thereisastateinthesystem,whichisthestartingstateofthesystem.

–(5)Therearesomestatesinthesystemthatindicatethatthecharacterstringithasreadsofarisasentenceofthelanguage.

Formaldefinition

·Definition:Afiniteautomaton(FA—finiteautomaton)isafive-tuple:

–M=(Q,Σ,δ,q0,F)

·Amongthem,

–Q——thenon-emptyfinitesetofstates.∀q∈Q,qiscalledastateofM.

–Σ——Enterthealphabet.

–δ——statetransitionfunction,sometimescalledstatetransitionfunctionormovementfunction,δ:Q×Σ→Q,δ(q,a)=p.

–q0——ThestartingstateofM,whichcanalsobecalledinitialstateorstartingstate.q0∈Q.

–F——M'sterminalstatecollection.FiscontainedbyQ.Letq∈F,qiscalledtheterminalstateofM.

Type

Therearemanytypesoffinitestateautomata:theacceptorjudgeswhethertoacceptinput;theconverterproducesanoutputforagiveninput.CommonconvertersareMooremachineandMealymachine.TheMooremachinehasanoutputactionattachedtoeachstate,andtheMealymachinehasanoutputactionattachedtoeachtransition.

Finitestateautomatacanalsobedividedintotwotypes:deterministicandnon-deterministic.Non-deterministicfinitestateautomatacanbetransformedintodeterministicfinitestateautomata.

Thelanguagerecognizedbythefinitestateautomataisaregularlanguage.

Inadditiontoitstheoreticalvalue,finitestateautomatahasalsobeenappliedinthefieldsofdigitalcircuitdesign,lexicalanalysis,texteditorprograms,etc.

AllthestringsacceptedbytheautomataconstitutethelanguageL(M)recognizedbytheautomata.

Non-deterministicfiniteautomaton

Anon-deterministicfiniteautomaton(NFA"Non-deterministicfiniteautomaton")Misafive-tuple(Q,Σ,δ,q0,F)

ThesetoffinitestatesQ;

ThefiniteinputalphabetΣ;

Transitionfunctionδ:Q×Σ->2Q;

Initialstateq0;

ThefinalstatesetF,FisincludedinQ.

Fromtheinitialstateq0,theautomatonreadseachletteroftheinputstring(consistingofthelettersoftheinputalphabetΣ)onebyone,anddeterminestheautomaton'slowerorderaccordingtothecurrentstate,theinputletterandthetransferfunctionδ.One-stepstate;iftheautomatonisinastateofthefinalstatesetFwhentheinputstringends,itmeansthattheautomatonacceptsthecharacterstring;otherwise,theautomatadoesnotacceptthecharacterstring.

Theonlydifferencebetweennon-deterministicfinitestateautomataanddeterministicfinitestateautomataistheirdifferenttransferfunctions.Makesurethatthefinitestateautomatonhasonlyonestatetransitionforeachpossibleinput.Thenon-deterministicfinitestateautomatoncanhavemultiplestatetransitionsforeachpossibleinput,andwhenreceivingtheinput,oneofthemultiplestatetransitionsisselectednon-deterministically.

AllthestringsacceptedbytheautomataconstitutethelanguageL(M)recognizedbytheautomata.

Computingpower

Thelanguages​​recognizedbydeterministicfinitestateautomataandnon-deterministicfinitestateautomataareregularlanguages.Duetothegoodnatureofregularlanguage,manyproblemscannotbedeterminedbyotherautomata(push-downautomataorTuringmachine).Inthecaseoffinitestateautomata,theycanallbedetermined,andthereareeffectivealgorithms.

Foradeterministicfinitestateautomaton,thefollowingdeterminationproblemscanbedetermined,andthereareeffectivealgorithms.

Whetherthelanguagerecognizedbythisautomatonisanemptyset.

Whetherthelanguagerecognizedbytheautomatonisafiniteset.

Doesthisautomatonrecognizethesamelanguageasanothercertainfinitestateautomaton?

Forexample:finitestateautomata:theinputstringisahexadecimalnumber,andtheoutputistheremainderofmodulo5(0,1,2,3,4)

theremainderofmodulo5Thereareonly5intotal,whichis5states.Theinitialstateis0,andeachstateisalsothefinalstate.

Thereare3possibilitiesforeachdigitoftheternarysystem,sothereare3transitionpossibilitiesforeachstate.

Understandtheternarystringasoneinputfromhightolow,eachinputisatransition,andthestateistheremainderoftheternarymodulo5uptothecurrentinput.

Thefunctionofthetransitionisasfollows:

Targetstate=(currentstate*hexadecimalnumber(thistitleis3)+thecurrentpositionofthestring)%5.

Theexampleisasfollows:

Ternarynumber12112

Currentstateinputtransition

0(start)1(0*3+1)%5=1

12(1*3+2)%5=0

01(0*3+1)%5=1

11(1*3+1)%5=4

42(4*3+2)%5=4(finalresult)

Minimize

AccordingtotheMyhill-Nerodetheorem,thedeterministicfinitestateautomatonthatacceptstheleaststateofaregularlanguageinthesenseofisomorphismisunique.Atthesametime,wealsohaveaneffectivealgorithm(timeoverheadisO(n^2))toconstructaminimumdeterministicfinitestateautomataequivalenttoagivendeterministicfinitestateautomata.