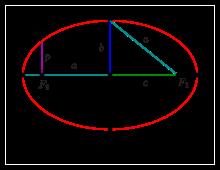
Ellipse geometry

Introduction

After the emergence of Verobachevsky’s geometry, in 1854, GFBRiemann stated that "crossing a point outside the straight line, no straight line is coplanar with the known straight line. "Disjoint" is the axiom to replace the Euclidean parallel axiom, creating another non-Euclidean geometry, which people call Riemannian geometry. Abbreviated as Li's geometry, also known as elliptic geometry. In this geometry, the sum of the inner angles of a triangle is greater than two right angles. Although non-Euclidean geometry and Euclidean geometry have different results, they are both non-contradictory geometry. Non-Euclidean geometry can even be expressed on some curved surfaces of Euclidean geometry. The emergence of non-Euclidean geometry breaks the uniqueness of geometric space and reflects the diversity of spatial forms. From the perspective of differential geometry, Euclidean geometry reflects a space with zero curvature, Lobachevsky geometry reflects a space with a negative curvature, and Riemannian geometry reflects a space with a positive curvature. These new discoveries have enabled people to make new progress in the understanding of space and expanded the scope of application of geometry. The discovery of non-Euclidean geometry is one of the most important mathematical achievements of the 19th century.

Elliptical geometry (6 photos)

Riemannian manifold

Riemann realizes that the metric is only a structure added to the manifold, and it is in the same manifold There can be many different metrics. Mathematicians before Riemann only knew that there is an induced metric ds²=Edu²+2Fdudv+Gdv² on the surface S in the three-dimensional Euclidean space E3, which is the first basic form, but did not realize that S can also be independent of three-dimensional Euclidean. The metric structure given by Guiridian Geometry. Riemann realized the importance of distinguishing between induced metric and independent Riemann metric, and thus got rid of the limitation of induced metric in classical differential geometry surface theory, and founded Riemannian geometry, which contributed to the development of modern mathematics and physics. Outstanding contribution.

Riemannian geometry takes Euclidean geometry and various non-Euclidean geometry as its special cases. For example: define a metric (a is a constant), then when a=0, it is ordinary Euclidean geometry, when a>0, it is elliptic geometry, and when a<0, it is hyperbolic geometry.

A basic problem in Riemannian geometry is the equivalence of differential forms. The problem was solved by E.B. Christofel and R. Lipschitz around 1869. The solution of the former includes two types of Christofel's notation named after his surname and the concept of covariant differential. On this basis, G. Rich developed a tensor analysis method, which played the role of a basic mathematical tool in general relativity. They further developed Riemannian geometry.

But in the era of Riemann, Lie groups and topology have not yet been developed, so Riemannian geometry is limited to a small range of theories. It was about 1925 that H. Hopf began to study the relationship between the differential structure and topological structure of Riemann space. With the establishment of the precise concept of differential manifolds, in particular, E. Cartan pioneered and developed the outer differential form and the active frame method in the 1920s, and established the connection between Lie groups and Riemannian geometry, which helped Li The development of Mange Geometry laid an important foundation and opened up a vast field with far-reaching influence. And thus developed the study of linear connections and fiber bundles.

In 1915, A. Einstein used Riemannian geometry and tensor analysis tools to create a new theory of gravity—General Relativity. Make Riemannian geometry (strictly speaking Lorentz geometry) and its operation method (Rich algorithm) become an effective mathematical tool for the study of general relativity. The development of the theory of relativity in recent years has been strongly influenced by the overall differential geometry. For example, vector bundles and connection theory constitute the mathematical basis of gauge fields (Yang-Mills field).

In 1944, Chen Xingshen gave the intrinsic proof of the Gauss-Bonnet formula of n-dimensional Riemannian manifolds, and his research on the indicative classes of Hermitian manifolds, introducing what was later commonly known as narrative Classes provide an indispensable tool for a wide range of differential geometry and create a precedent for the study of differential geometry and topology of complex manifolds. For more than half a century, the research of Riemannian geometry has developed from part to whole, and has produced many profound results. Riemannian geometry and partial differential equations, multi-complex variable function theory, algebraic topology and other disciplines interpenetrate and influence each other, and play a major role in modern mathematics and theoretical physics.